DeepXDE
DeepXDE is a library for scientific machine learning and physics-informed learning. DeepXDE includes the following algorithms:
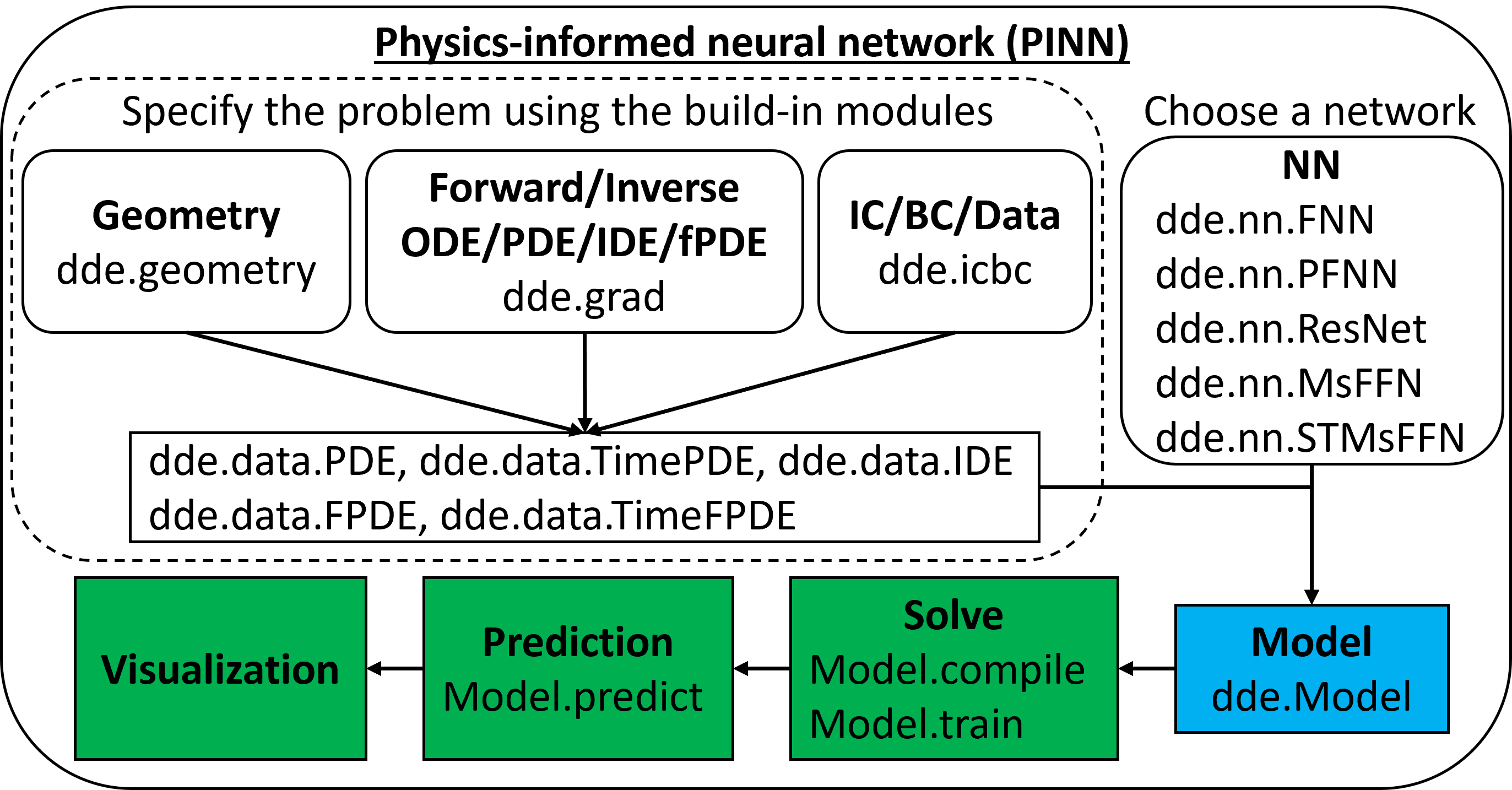
- physics-informed neural network (PINN)
- solving different problems
solving forward/inverse ordinary/partial differential equations (ODEs/PDEs) [SIAM Rev.]
solving forward/inverse integro-differential equations (IDEs) [SIAM Rev.]
fPINN: solving forward/inverse fractional PDEs (fPDEs) [SIAM J. Sci. Comput.]
NN-arbitrary polynomial chaos (NN-aPC): solving forward/inverse stochastic PDEs (sPDEs) [J. Comput. Phys.]
PINN with hard constraints (hPINN): solving inverse design/topology optimization [SIAM J. Sci. Comput.]
- improving PINN accuracy
residual-based adaptive sampling [SIAM Rev., Comput. Methods Appl. Mech. Eng.]
gradient-enhanced PINN (gPINN) [Comput. Methods Appl. Mech. Eng.]
PINN with multi-scale Fourier features [Comput. Methods Appl. Mech. Eng.]
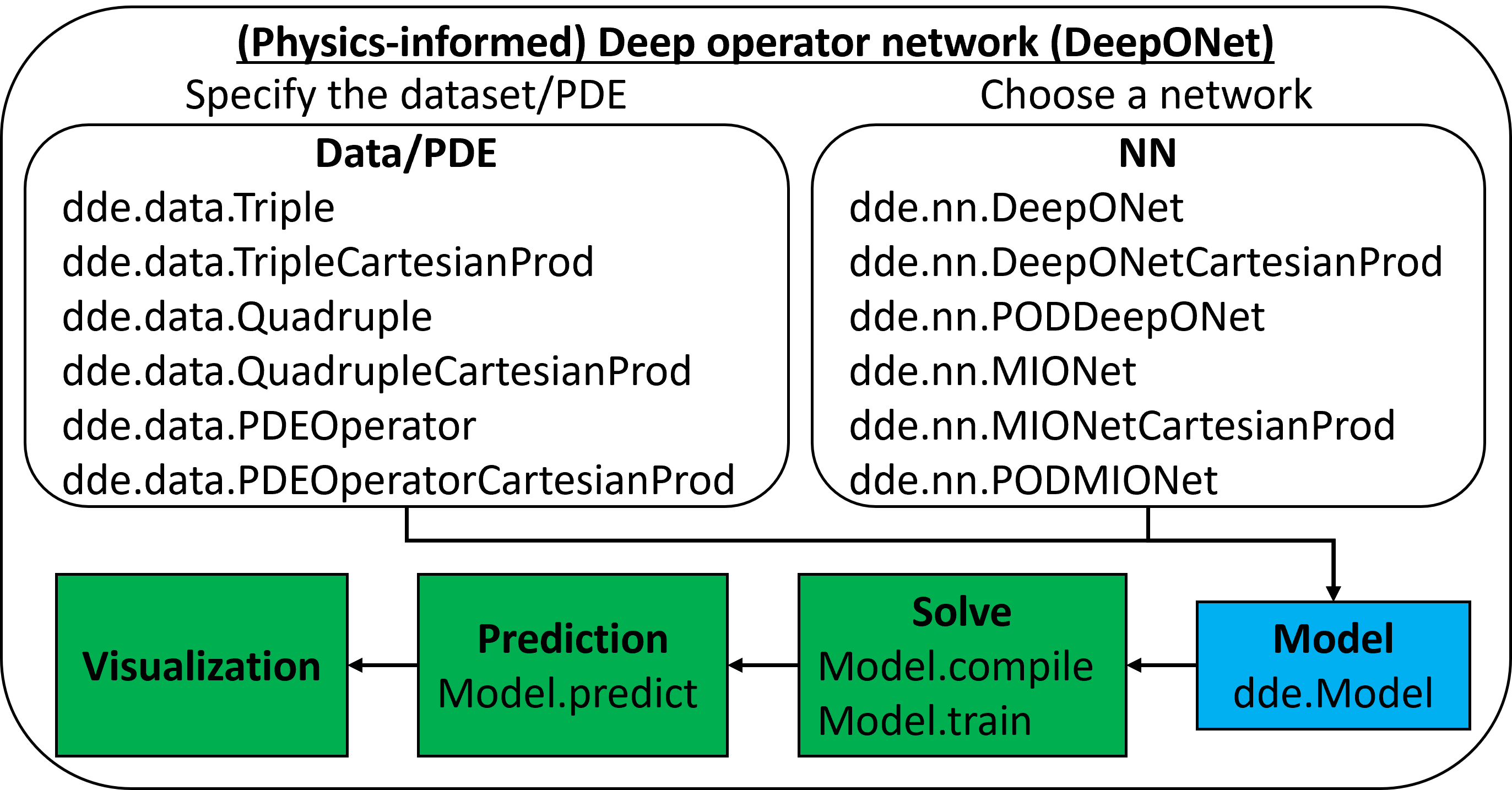
- (physics-informed) deep operator network (DeepONet)
DeepONet: learning operators [Nat. Mach. Intell.]
DeepONet extensions, e.g., POD-DeepONet [Comput. Methods Appl. Mech. Eng.]
MIONet: learning multiple-input operators [SIAM J. Sci. Comput.]
Fourier-DeepONet [Comput. Methods Appl. Mech. Eng.], Fourier-MIONet [arXiv]
physics-informed DeepONet [Sci. Adv.]
multifidelity DeepONet [Phys. Rev. Research]
DeepM&Mnet: solving multiphysics and multiscale problems [J. Comput. Phys., J. Comput. Phys.]
Reliable extrapolation [Comput. Methods Appl. Mech. Eng.]
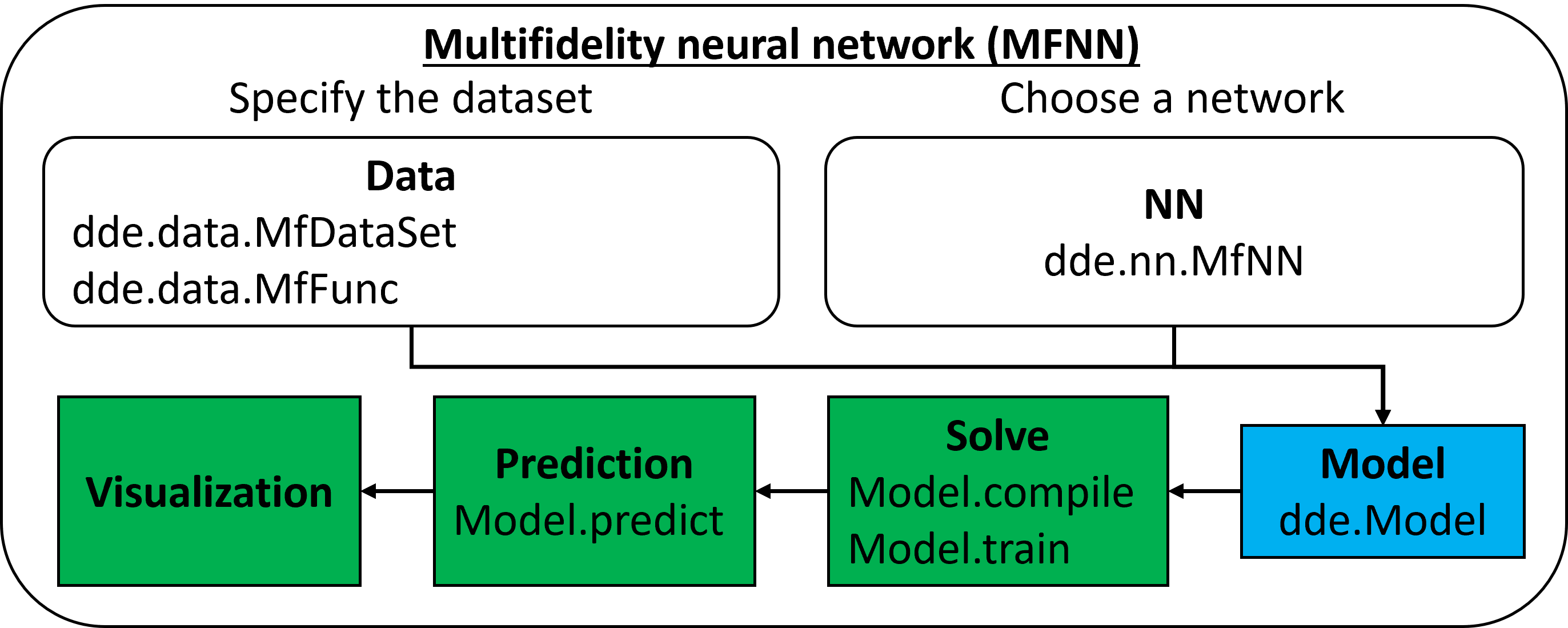
- multifidelity neural network (MFNN)
learning from multifidelity data [J. Comput. Phys., PNAS]
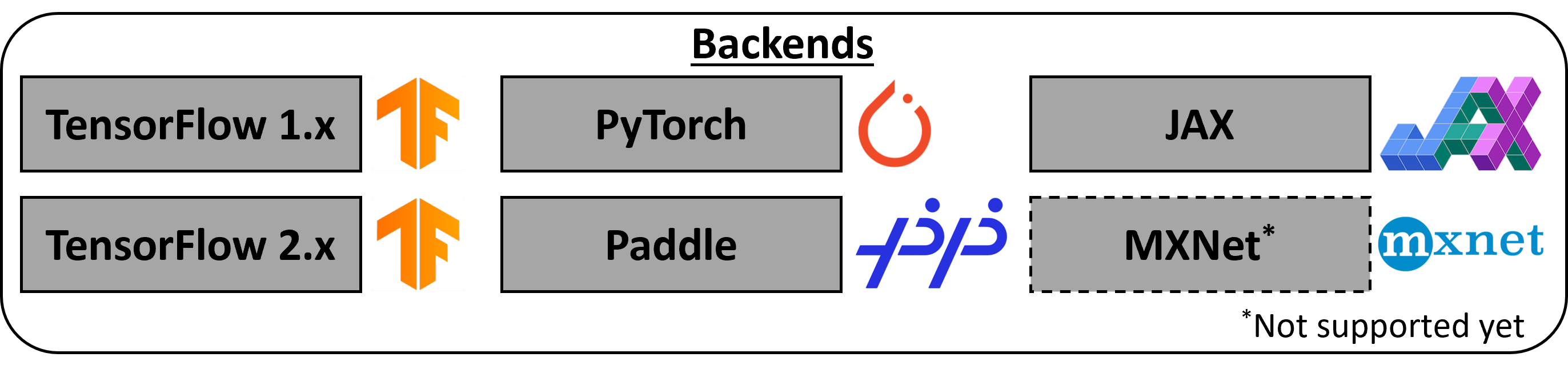
DeepXDE supports five tensor libraries as backends: TensorFlow 1.x (tensorflow.compat.v1 in TensorFlow 2.x), TensorFlow 2.x, PyTorch, JAX, and PaddlePaddle. For how to select one, see Working with different backends.
Documentation: ReadTheDocs
Features
DeepXDE has implemented many algorithms as shown above and supports many features:
enables the user code to be compact, resembling closely the mathematical formulation.
complex domain geometries without tyranny mesh generation. The primitive geometries are interval, triangle, rectangle, polygon, disk, ellipse, star-shaped, cuboid, sphere, hypercube, and hypersphere. Other geometries can be constructed as constructive solid geometry (CSG) using three boolean operations: union, difference, and intersection. DeepXDE also supports a geometry represented by a point cloud.
5 types of boundary conditions (BCs): Dirichlet, Neumann, Robin, periodic, and a general BC, which can be defined on an arbitrary domain or on a point set; and approximate distance functions for hard constraints.
3 automatic differentiation (AD) methods to compute derivatives: reverse mode (i.e., backpropagation), forward mode, and zero coordinate shift (ZCS).
different neural networks: fully connected neural network (FNN), stacked FNN, residual neural network, (spatio-temporal) multi-scale Fourier feature networks, etc.
many sampling methods: uniform, pseudorandom, Latin hypercube sampling, Halton sequence, Hammersley sequence, and Sobol sequence. The training points can keep the same during training or be resampled (adaptively) every certain iterations.
4 function spaces: power series, Chebyshev polynomial, Gaussian random field (1D/2D).
data-parallel training on multiple GPUs.
different optimizers: Adam, L-BFGS, etc.
conveniently save the model during training, and load a trained model.
callbacks to monitor the internal states and statistics of the model during training: early stopping, etc.
uncertainty quantification using dropout.
float16, float32, and float64.
many other useful features: different (weighted) losses, learning rate schedules, metrics, etc.
All the components of DeepXDE are loosely coupled, and thus DeepXDE is well-structured and highly configurable. It is easy to customize DeepXDE to meet new demands.
User guide
API reference
If you are looking for information on a specific function, class or method, this part of the documentation is for you.
API
- deepxde
- deepxde.data
- deepxde.data.constraint module
- deepxde.data.data module
- deepxde.data.dataset module
- deepxde.data.fpde module
- deepxde.data.func_constraint module
- deepxde.data.function module
- deepxde.data.function_spaces module
- deepxde.data.helper module
- deepxde.data.ide module
- deepxde.data.mf module
- deepxde.data.pde module
- deepxde.data.pde_operator module
- deepxde.data.quadruple module
- deepxde.data.sampler module
- deepxde.data.triple module
- deepxde.geometry
- deepxde.geometry.csg module
- deepxde.geometry.geometry module
- deepxde.geometry.geometry_1d module
- deepxde.geometry.geometry_2d module
- deepxde.geometry.geometry_3d module
- deepxde.geometry.geometry_nd module
- deepxde.geometry.pointcloud module
- deepxde.geometry.sampler module
- deepxde.geometry.timedomain module
- deepxde.gradients
- deepxde.icbc
- deepxde.nn
- deepxde.nn.jax
- deepxde.nn.paddle
- deepxde.nn.pytorch
- deepxde.nn.tensorflow
- deepxde.nn.tensorflow_compat_v1
- deepxde.nn.tensorflow_compat_v1.deeponet module
- deepxde.nn.tensorflow_compat_v1.fnn module
- deepxde.nn.tensorflow_compat_v1.mfnn module
- deepxde.nn.tensorflow_compat_v1.mionet module
- deepxde.nn.tensorflow_compat_v1.msffn module
- deepxde.nn.tensorflow_compat_v1.nn module
- deepxde.nn.tensorflow_compat_v1.resnet module
- deepxde.optimizers
- deepxde.utils